Activities/Turtle Art/Tutorials

Tutorials

Tony Forster's Blog

Tony Forster has written a number of blog posts about his experiments with Turtle Art:

• Using Python blocks in TurtleArt
• Turtle Lander
• Reprogramming Sugar
• Turtle random File:Turtle Blocks Activity random.ta (English & español)
• Turtle random V2 File:Turtle Blocks Activity randomv3.ta (English & español)
• Turtle Lissajous File:Turtle Art lisajous.ta (English & español)
• Turtle spring damper File:Turtle spring damper.ta (English & español)
• color and shade
• Turtle Art shapes
• Bouncing Turtle File:TurtleArt bounce.ta
• Turtle Pythagoras 1, 2
• Turtle graph File:Turtle graph.ta
• Turtle Pi File:Turtle pi.ta (English & español)
• Turtle Pi, another one File:Turtle Blocks pi another.ta (English & español)
• Turtle fractions File:TmpBtvKZX.ta (English & español)
• Turtle interactive multimedia
• capture numeric input File:Turtle Art getnumber.ta (English & español)
• Turtle eFile:Turtle e.ta (English & español)
• Turtle spirograph File:Turtle Art spirograph.ta (English & español)
• Mouse support File:Turtle Art Activity mouse.ta
• Turtle-sieve-of-Eratosthenes File:Turtle Art Activity eratos.ta (English & español)
• Turtle sliderule
• Turtle Diophantine File:Turtle Blocks Activity Diophantine.ta, see also (English & español)
• Turtle Paint File:Turtle Blocks Activity paint.doc
• Turtle Music Keyboard File:Turtle Art Activity keyboard.doc (English & español)
• Text to speech
• Talking clock File:Talking clock.ta
• Pie chart File:Turtle Art Activity pie chart.ta
• Singing turtle
• screen broadcast
• Maths, flip and rotate File:Flipandrotate.ta
• Maths, fractions and decimals File:Turtle Art Activity baloon0-1.ta Multiplication <100 File:Baloon100.ta Counting File:Count1-9.ta
• A simple die or spinner for probability File:Turtle Art Activity spinner.ta
• Division drill File:Turtle Art Activity division drill.ta
• Turtle calculus
• Turtle serial USB
• Graphing pitch and volume
• Orbital motion File:Turtle Art Activity orbital.ta

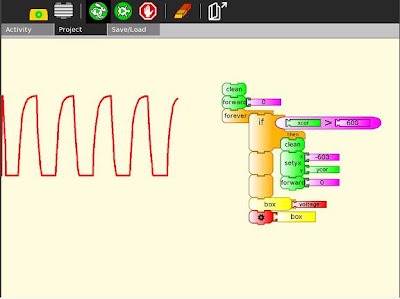
An bringing it all together, the Turtle Art Oscilloscope.

Tony has also used the programmable block to do file IO.

Video Tutorials

I know there are a few but they are not categorized on this page... we'll make that happen soon. Help would be appreciated.

• introductory videos here on Turtle Art
• To Square—a tutorial by the Summer Spot youths at the Lilla G. Frederick Pilot Middle School
• A basic tutorial.
• a video of the portfolio basics
• Get your hot cold Turtle Art Video here!
• Name that State!
• A Shapes and Colors Game

Mokurai's Tutorials

Mokurai has been working on how to teach Sugar by guided discovery, rather than by explicit direction, with only the necessary minimum of hints. At the same time, he has been working on Turtle Art examples to teach concepts of mathematics, programming, Computer Science, and physics, aiming where possible at presentations suitable for pre-literate pre-schoolers. Thus, no text, no formulas, no calculations. Those can come later in sequences on the same topics as children develop, including a transition from Turtle Art to Python, Logo, and Smalltalk, with options for other languages. However, it is necessary to provide texts, sometimes with formulas and calculations, for the teacher or parent helping the child. These will appear on Mokurai's Replacing Textbooks blog, available at PlanetSugarlabs, and will be incorporated into Open Education Resources on the Sugar Labs Replacing Textbooks server.

Planned topics

Pre-school

• You be the Turtle
• Turtle Art programming without words (includes Mayan and other visual numerals)
• Spirograph
• Counting
• Mathematics and art
• Conservation of number
• Figurate numbers
• Elementary arithmetic with whole numbers (but no numerals)
• Shortcuts to the times table
• Abacus and Chisanpeop (abacus on fingers)
• Fractions with cake and pie slices
• Infinite sequences and series
• Groups of symmetries
• Permutations and permutation groups
• The ring of clock time
• The fields of rationals and reals
• Knots and braids (and knitting, crocheting, macramé, tatting...)
• Kindergarten Calculus (tangents, areas, maxima and minima...)
• Adding Apples and Oranges
• Vectors
• Venn diagrams
• Euclid, Book I: triangles, parallelograms, squares
• Spherical geometry (Riemann)
• Pseudospherical geometry (Lobachevsky)
• Projective geometry
• Geometric optics
• Moiré patterns and interference
• Tilings
• Topology (Rubber-sheet geometry)
• Juggling
• The square circle and other metrics
• Periodic and almost-periodic functions (Lissajous figures)
• Maps
• Iterated functions (attractors, chaos)
• Fractals
• Stack programming
• Parse trees
• Probability
• Combinatorics
• Models of simple molecules
• Moving between Turtle Art and the physical world

Primary school

• Algorithms of arithmetic
• Numerals
• Learning math by teaching the computer
• Galilean gravity
• Galilean relativity
• Measuring slopes of tangents
• Approximate integrals
• Python blocks
• Transition to Python
• Create your own Turtle Art add-ons in Python
• Turtle Graphics in Smalltalk
• Transition to Smalltalk
• Saving Turtle Art programs in Logo
• Transition to Logo
• Frieze groups
• 3D tilings and crystallographic groups
• Coordinate geometry, Cartesian and Polar
• Conditional probabilities
• Elementary statistics
• Models of complex molecules; nomenclature

Higher

At this level it is not necessary to use Turtle Art to introduce ideas. Nevertheless the ability to display a topic in Turtle Art demonstrates that it is of only a moderate level of complexity.

• The Chomsky hierarchy of machines and languages
  • Finite state machine/automaton
  • Stack machine or pushdown automaton
  • Bounded linear automaton
  • Turtle Art Turing Machine
• Algebra
• Trigonometry
• 3D coordinate geometry
• Elementary differential equations
• Electric and magnetic fields
• Algebraic structures
• Statistical analysis