Difference between revisions of "Activities/Abacus/Worksheet/Answersheet"
Tonyforster (talk | contribs) |
Tonyforster (talk | contribs) |
||
| Line 10: | Line 10: | ||
Ways to make 1/2 with more than one string | Ways to make 1/2 with more than one string | ||
| − | 1/3 + 1/6 | + | 1/3 + 1/6 = (2+1)/6 = 3/6 = 1/2 |
| − | 1/3 + 2/12 | + | 1/3 + 2/12 = (4+2)/12 = 6/12 = 1/2 |
| − | 1/4 + 1/6 + 1/12 | + | 1/4 + 1/6 + 1/12 = (3+2+1)/12 = 6/12 = 1/2 |
| − | 1/4 + 2/8 | + | 1/4 + 2/8 = (2+2)/8 = 4/8 = 1/2 |
| − | 1/4 + 3/12 | + | 1/4 + 3/12 = (3+3)/12 = 6/12 = 1/2 |
| − | 3/9 + 2/12 | + | 3/9 + 2/12 = (12+6)/36 = 18/36 = 1/2 |
| − | 2/8 + 3/12 | + | 2/8 + 3/12 = 1/4 + 1/4 = 1/2 |
| − | 1/6 + 4/12 | + | 1/6 + 4/12 = (2+4)/12 = 6/12 = 1/2 |
| − | 1/6 + 3/9 | + | 1/6 + 3/9 = (3+6)/18 = 9/18 = 1/2 |
| − | 1/6 + 2/8 + 1/12 | + | 1/6 + 2/8 + 1/12 = (4+6+2)/24 = 12/24 = 1/2 |
| − | 2/6 + 2/12 | + | 2/6 + 2/12 = (2+1)/6 = 3/6 = 1/2 |
| − | 1/5 + 3/10 | + | 1/5 + 3/10 = (2+3)/10 = 5/10 =1/2 |
| − | 2/5 + 1/10 | + | 2/5 + 1/10 = (4+1)/10 = 5/10 =1/2 |
| Line 41: | Line 41: | ||
See [http://en.wikipedia.org/wiki/Diophantine_equation Diophantine equations], computer programs [http://tonyforster.blogspot.com/2010/09/turtle-diophantine.html including ones written in TurtleArt] can find all the solutions by trial and error. | See [http://en.wikipedia.org/wiki/Diophantine_equation Diophantine equations], computer programs [http://tonyforster.blogspot.com/2010/09/turtle-diophantine.html including ones written in TurtleArt] can find all the solutions by trial and error. | ||
| − | + | You can paste [[File:Turtle Art Activity fraction diophantine.ta |this code]] into Turtle Art to calculate all the possibilities | |
| − | |||
===Ways to make 1/3=== | ===Ways to make 1/3=== | ||
Revision as of 20:32, 5 April 2011
Answers to the Abacus Worksheet
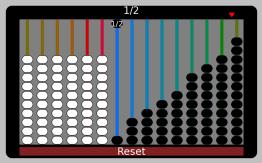
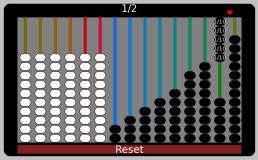
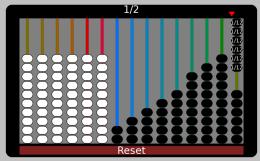
Ways to make 1/2
Ways to make 1/2 just using one string
To make 1/2 just using one string, the fraction denominator must be divisible by 2. The string must contain an even number of beads, 2 4 6 8 10 12
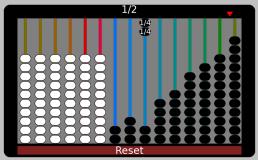
Ways to make 1/2 with more than one string
1/3 + 1/6 = (2+1)/6 = 3/6 = 1/2
1/3 + 2/12 = (4+2)/12 = 6/12 = 1/2
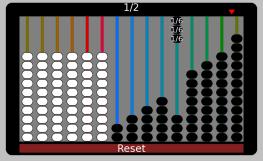
1/4 + 1/6 + 1/12 = (3+2+1)/12 = 6/12 = 1/2
1/4 + 2/8 = (2+2)/8 = 4/8 = 1/2
1/4 + 3/12 = (3+3)/12 = 6/12 = 1/2
3/9 + 2/12 = (12+6)/36 = 18/36 = 1/2
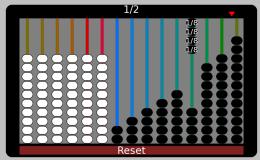
2/8 + 3/12 = 1/4 + 1/4 = 1/2
1/6 + 4/12 = (2+4)/12 = 6/12 = 1/2
1/6 + 3/9 = (3+6)/18 = 9/18 = 1/2
1/6 + 2/8 + 1/12 = (4+6+2)/24 = 12/24 = 1/2
2/6 + 2/12 = (2+1)/6 = 3/6 = 1/2
1/5 + 3/10 = (2+3)/10 = 5/10 =1/2
2/5 + 1/10 = (4+1)/10 = 5/10 =1/2
Is this all of the possibilities?
See Diophantine equations, computer programs including ones written in TurtleArt can find all the solutions by trial and error.
You can paste File:Turtle Art Activity fraction diophantine.ta into Turtle Art to calculate all the possibilities
Ways to make 1/3
This program can be modified for 1/3 and 2/3 (and with more work it could be used for the Caacupé abacus). Circled below, the program above has 0.5 replaced with 1/3 to find the ways of making 1/3
4/12
3/9
2/8 + 1/12
1/6 + 2/12
2/6
1/4 + 1/12
1/3