Activities/Turtle in a Pond: Difference between revisions
| Line 35: | Line 35: | ||
Cut and paste these examples into Pippy and save then to your Sugar Journal. Then use the Load-strategy button in Turtle in a Pond to try them. | Cut and paste these examples into Pippy and save then to your Sugar Journal. Then use the Load-strategy button in Turtle in a Pond to try them. | ||
In this strategy, the turtle moves down | In this strategy, the turtle moves down regardless of whether the dot is open. | ||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
| Line 42: | Line 42: | ||
</pre> | </pre> | ||
In this strategy, the turtle moves down until it is blocked (i.e., when the dot type | In this strategy, the turtle moves down until it is blocked (i.e., when the dot type is True). | ||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
| Line 55: | Line 55: | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
evenodd = turtle[1] % 2 | evenodd = turtle[1] % 2 | ||
for i in range(6): | for i in range(6): # search for an opening | ||
column = turtle[0] + CIRCLE[evenodd][i][0] | column = turtle[0] + CIRCLE[evenodd][i][0] | ||
row = turtle[1] + CIRCLE[evenodd][i][1] | row = turtle[1] + CIRCLE[evenodd][i][1] | ||
| Line 68: | Line 68: | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
evenodd = turtle[1] % 2 | evenodd = turtle[1] % 2 | ||
for i in range(6): | for i in range(6): # search for an opening | ||
column = turtle[0] + CIRCLE[evenodd][i][0] | column = turtle[0] + CIRCLE[evenodd][i][0] | ||
row = turtle[1] + CIRCLE[evenodd][i][1] | row = turtle[1] + CIRCLE[evenodd][i][1] | ||
| Line 82: | Line 82: | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
evenodd = turtle[1] % 2 | evenodd = turtle[1] % 2 | ||
n = int(uniform(0, 6)) | n = int(uniform(0, 6)) # choose a random orientation | ||
for i in range(6): | for i in range(6): | ||
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | ||
| Line 97: | Line 97: | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
evenodd = turtle[1] % 2 | evenodd = turtle[1] % 2 | ||
for i in range(6): | for i in range(6): # look for an edge to escape to | ||
column = turtle[0] + CIRCLE[evenodd][i][0] | column = turtle[0] + CIRCLE[evenodd][i][0] | ||
row = turtle[1] + CIRCLE[evenodd][i][1] | row = turtle[1] + CIRCLE[evenodd][i][1] | ||
| Line 104: | Line 104: | ||
return [column, row] | return [column, row] | ||
n = int(uniform(0, 6)) | n = int(uniform(0, 6)) # choose a random orientation | ||
for i in range(6): | for i in range(6): | ||
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | ||
| Line 114: | Line 114: | ||
</pre> | </pre> | ||
If it tries to continue in the direction it was already heading, the turtle is harder to catch. | If it mostly tries to continue in the direction it was already heading, the turtle is harder to catch. | ||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
evenodd = turtle[1] % 2 | evenodd = turtle[1] % 2 | ||
column = turtle[0] + CIRCLE[evenodd][self._orientation][0] | if int(uniform(0, 2)) > 0: # mostly try going straight | ||
column = turtle[0] + CIRCLE[evenodd][self._orientation][0] | |||
row = turtle[1] + CIRCLE[evenodd][self._orientation][1] | |||
if not self._dots[self._grid_to_dot((col, row))].type: | |||
n = int(uniform(0, 6)) | return [col, row] | ||
n = int(uniform(0, 6)) # choose a random orientation | |||
for i in range(6): | for i in range(6): | ||
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0] | ||
Revision as of 13:17, 30 November 2011
Turtle in a Pond Activity
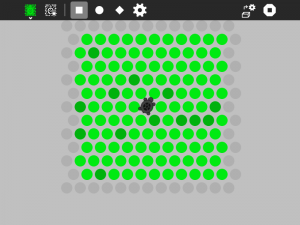
Turtle in a Pond is a strategy game. The goal is to surround the turtle before it runs of the screen.
How to play Turtle in a Pond
Click on the dots to keep the turtle from escaping.
-
The turtle is captured
-
The turtle escaped
Did you know that:
The Toolbars
- from left to right
- the Activity toolbar button (shown in the open position)
- the New-game button
- an area for messages
- the Load-new-strategy button
- the Reload-the-default-strategy button
- the Activity stop button
Strategy
Cut and paste these examples into Pippy and save then to your Sugar Journal. Then use the Load-strategy button in Turtle in a Pond to try them.
In this strategy, the turtle moves down regardless of whether the dot is open.
def _turtle_strategy(self, turtle):
turtle[1] += 1
return turtle
In this strategy, the turtle moves down until it is blocked (i.e., when the dot type is True).
def _turtle_strategy(self, turtle):
if not self._dots[self._grid_to_dot((turtle[0], turtle[1]+1))].type:
turtle[1] += 1
return turtle
In this strategy, the turtle searches for an open dot, looking clockwise.
def _turtle_strategy(self, turtle):
evenodd = turtle[1] % 2
for i in range(6): # search for an opening
column = turtle[0] + CIRCLE[evenodd][i][0]
row = turtle[1] + CIRCLE[evenodd][i][1]
if not self._dots[self._grid_to_dot((column, row))].type:
return [column, row]
return turtle
In this version, the turtle orientation is set as well.
def _turtle_strategy(self, turtle):
evenodd = turtle[1] % 2
for i in range(6): # search for an opening
column = turtle[0] + CIRCLE[evenodd][i][0]
row = turtle[1] + CIRCLE[evenodd][i][1]
if not self._dots[self._grid_to_dot((column, row))].type:
self._orientation = i
return [column, row]
return turtle
In the default strategy, the turtle choose a random direction and goes there if the dot is open.
def _turtle_strategy(self, turtle):
evenodd = turtle[1] % 2
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6):
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0]
row = turtle[1] + CIRCLE[evenodd][(i + n) % 6][1]
if not self._dots[self._grid_to_dot((column, row))].type:
self._orientation = (i + n) % 6
return [column, row]
return turtle
In this strategy, the turtle will go off the edge if it can.
def _turtle_strategy(self, turtle):
evenodd = turtle[1] % 2
for i in range(6): # look for an edge to escape to
column = turtle[0] + CIRCLE[evenodd][i][0]
row = turtle[1] + CIRCLE[evenodd][i][1]
if self._dots[self._grid_to_dot((column, row))].type is None:
self._orientation = i
return [column, row]
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6):
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0]
row = turtle[1] + CIRCLE[evenodd][(i + n) % 6][1]
if not self._dots[self._grid_to_dot((column, row))].type:
self._orientation = (i + n) % 6
return [column, row]
return turtle
If it mostly tries to continue in the direction it was already heading, the turtle is harder to catch.
def _turtle_strategy(self, turtle):
evenodd = turtle[1] % 2
if int(uniform(0, 2)) > 0: # mostly try going straight
column = turtle[0] + CIRCLE[evenodd][self._orientation][0]
row = turtle[1] + CIRCLE[evenodd][self._orientation][1]
if not self._dots[self._grid_to_dot((col, row))].type:
return [col, row]
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6):
column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0]
row = turtle[1] + CIRCLE[evenodd][(i + n) % 6][1]
if not self._dots[self._grid_to_dot((column, row))].type:
self._orientation = (i + n) % 6
return [column, row]
return turtle
The dots are stored in a 13✕13 array. Each dot has an attribute, 'type', that determines it status. The edges have a type=None. Occupied dots have a type=True. Unoccupied dots have a type=False.
Your strategy should start with:
def _turtle_strategy(self, turtle):
The turtle argument is a tuple containing the column and row of the current turtle position. That is, turtle[0] is the horizontal position and turtle[1] is the vertical position.
Your strategy should return a tuple containing the column and row of the new turtle position, e.g.,
return [column, row]
There are some resources that you can use in your program, including:
- self._dots
- the array of dots from which you can test the type attribute (self._dots[i].type==None → edge; self._dots[i].type==False → open; self._dots[i].type==True → blocked)
- self._orientation
- you can set the orientation of your turtle by assigning a number from 0-5 (clockwise beginning with 30 degrees from north)
- self._set_label('your message here')
- you can write a message on the toolbar if you want to communicate what your turtle is thinking
- self._grid_to_dot((column, row))
- returns the dot that is at a grid position (column, row)
- self._dot_to_grid(dot)
- returns an array (column, row) representing the grid position of a dot
- CIRCLE
- a 2✕6✕2 array of offsets that can used to find the column and row of the dots surrounding the turtle.
A bit more explanation about the CIRCLE constant:
CIRCLE contains tuples of offsets (a column offset and a row offset) that allow you to find the grid coordinates (column and row) of the 6 dots that surround the turtle. It is complicated by the fact that the rows are staggered (in order to form hexagons) so when the turtle is on an even row (turtle[1] % 2 == 0) we use one set of offsets (CIRCLE[0]) and when it is on an odd row (turtle[1] % 2 == 1) we use a second set of offsets (CIRCLE[1]).
Where to get Turtle in a Pond
The Turtle in a Pond activity is available for download from the Sugar activity portal: Turtle in a Pond
The source code is available on the Sugar Labs Gitorious server.