Activities/Turtle in a Pond: Difference between revisions
| Line 54: | Line 54: | ||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
dots = self._surrounding_dots(turtle) | |||
for i in range(6): # search for an opening | for i in range(6): # search for an opening | ||
if not self._dots[dots[i]].type: | |||
return self._dot_to_grid(dots[i]) | |||
if not self._dots[ | |||
return [ | |||
return turtle | return turtle | ||
</pre> | </pre> | ||
| Line 66: | Line 64: | ||
<pre> | <pre> | ||
dots = self._surrounding_dots(turtle) | |||
for i in range(6): # search for an opening | for i in range(6): # search for an opening | ||
if not self._dots[dots[i]].type: | |||
if not self._dots[ | |||
self._orientation = i | self._orientation = i | ||
return [ | return self._dot_to_grid(dots[i]) | ||
return turtle | return turtle | ||
</pre> | </pre> | ||
The turtle choose a random direction and goes there if the dot is open. | |||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
dots = self._surrounding_dots(turtle) | |||
n = int(uniform(0, 6)) # choose a random orientation | n = int(uniform(0, 6)) # choose a random orientation | ||
for i in range(6): | for i in range(6): # search for an opening | ||
if not self._dots[dots[(i + n) % 6]].type: | |||
self._orientation = (i + n) % 6 | self._orientation = (i + n) % 6 | ||
return [ | return self._dot_to_grid(dots[(i + n) % 6]) | ||
return turtle | return turtle | ||
</pre> | </pre> | ||
| Line 96: | Line 89: | ||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
dots = self._surrounding_dots(turtle) | |||
for i in range(6): # | for i in range(6): # search for an edge | ||
if self._dots[dots[i]].type is None: | |||
if self._dots[ | |||
self._orientation = i | self._orientation = i | ||
return [ | return self._dot_to_grid(dots[i]) | ||
n = int(uniform(0, 6)) # choose a random orientation | n = int(uniform(0, 6)) # choose a random orientation | ||
for i in range(6): | for i in range(6): # search for an opening | ||
if not self._dots[dots[(i + n) % 6]].type: | |||
self._orientation = (i + n) % 6 | self._orientation = (i + n) % 6 | ||
return [ | return self._dot_to_grid(dots[(i + n) % 6]) | ||
return turtle | return turtle | ||
</pre> | </pre> | ||
In the '''default strategy''', it looks for a path to the edge in the direction it was already heading. | |||
<pre> | <pre> | ||
def _turtle_strategy(self, turtle): | def _turtle_strategy(self, turtle): | ||
dots = self._surrounding_dots(turtle) | |||
for i in range(6): # search for an edge | |||
if self._dots[dots[i]].type is None: | |||
self._orientation = i | |||
return self._dot_to_grid(dots[i]) | |||
if self._daylight_ahead(turtle): | |||
return self._dot_to_grid(dots[self._orientation]) | |||
n = int(uniform(0, 6)) # choose a random orientation | n = int(uniform(0, 6)) # choose a random orientation | ||
for i in range(6): | for i in range(6): # search for an opening | ||
if not self._dots[dots[(i + n) % 6]].type: | |||
self._orientation = (i + n) % 6 | self._orientation = (i + n) % 6 | ||
return [ | return self._dot_to_grid(dots[(i + n) % 6]) | ||
return turtle | return turtle | ||
</pre> | </pre> | ||
| Line 148: | Line 139: | ||
There are some resources that you can use in your program, including: | There are some resources that you can use in your program, including: | ||
;self._surrounding_dots((column, row)): returns an array of dots surrounding a given position in the grid | |||
;self._daylight_ahead((column, row)): returns True if there is a clear path to the edge heading in the current direction | |||
;self._dots: the array of dots from which you can test the type attribute (self._dots[i].type==None → edge; self._dots[i].type==False → open; self._dots[i].type==True → blocked) | ;self._dots: the array of dots from which you can test the type attribute (self._dots[i].type==None → edge; self._dots[i].type==False → open; self._dots[i].type==True → blocked) | ||
;self._orientation:you can set the orientation of your turtle by assigning a number from 0-5 (clockwise beginning with 30 degrees from north) | ;self._orientation:you can set the orientation of your turtle by assigning a number from 0-5 (clockwise beginning with 30 degrees from north) | ||
| Line 153: | Line 146: | ||
;self._grid_to_dot((column, row)): returns the dot that is at a grid position (column, row) | ;self._grid_to_dot((column, row)): returns the dot that is at a grid position (column, row) | ||
;self._dot_to_grid(dot): returns an array (column, row) representing the grid position of a dot | ;self._dot_to_grid(dot): returns an array (column, row) representing the grid position of a dot | ||
=== Where to get Turtle in a Pond === | === Where to get Turtle in a Pond === | ||
Revision as of 16:23, 30 November 2011
Turtle in a Pond Activity
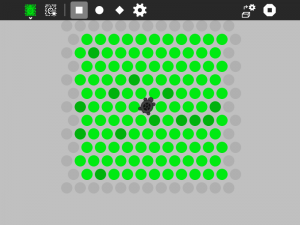
Turtle in a Pond is a strategy game. The goal is to surround the turtle before it runs of the screen.
How to play Turtle in a Pond
Click on the dots to keep the turtle from escaping.
-
The turtle is captured
-
The turtle escaped
Did you know that:
The Toolbars
- from left to right
- the Activity toolbar button (shown in the open position)
- the New-game button
- an area for messages
- the Load-new-strategy button
- the Reload-the-default-strategy button
- the Activity stop button
Strategy
Cut and paste these examples into Pippy and save then to your Sugar Journal. Then use the Load-strategy button in Turtle in a Pond to try them.
In this strategy, the turtle moves down regardless of whether the dot is open.
def _turtle_strategy(self, turtle):
turtle[1] += 1
return turtle
In this strategy, the turtle moves down until it is blocked (i.e., when the dot type is True).
def _turtle_strategy(self, turtle):
if not self._dots[self._grid_to_dot((turtle[0], turtle[1]+1))].type:
turtle[1] += 1
return turtle
In this strategy, the turtle searches for an open dot, looking clockwise.
def _turtle_strategy(self, turtle):
dots = self._surrounding_dots(turtle)
for i in range(6): # search for an opening
if not self._dots[dots[i]].type:
return self._dot_to_grid(dots[i])
return turtle
In this version, the turtle orientation is set as well.
dots = self._surrounding_dots(turtle)
for i in range(6): # search for an opening
if not self._dots[dots[i]].type:
self._orientation = i
return self._dot_to_grid(dots[i])
return turtle
The turtle choose a random direction and goes there if the dot is open.
def _turtle_strategy(self, turtle):
dots = self._surrounding_dots(turtle)
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6): # search for an opening
if not self._dots[dots[(i + n) % 6]].type:
self._orientation = (i + n) % 6
return self._dot_to_grid(dots[(i + n) % 6])
return turtle
In this strategy, the turtle will go off the edge if it can.
def _turtle_strategy(self, turtle):
dots = self._surrounding_dots(turtle)
for i in range(6): # search for an edge
if self._dots[dots[i]].type is None:
self._orientation = i
return self._dot_to_grid(dots[i])
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6): # search for an opening
if not self._dots[dots[(i + n) % 6]].type:
self._orientation = (i + n) % 6
return self._dot_to_grid(dots[(i + n) % 6])
return turtle
In the default strategy, it looks for a path to the edge in the direction it was already heading.
def _turtle_strategy(self, turtle):
dots = self._surrounding_dots(turtle)
for i in range(6): # search for an edge
if self._dots[dots[i]].type is None:
self._orientation = i
return self._dot_to_grid(dots[i])
if self._daylight_ahead(turtle):
return self._dot_to_grid(dots[self._orientation])
n = int(uniform(0, 6)) # choose a random orientation
for i in range(6): # search for an opening
if not self._dots[dots[(i + n) % 6]].type:
self._orientation = (i + n) % 6
return self._dot_to_grid(dots[(i + n) % 6])
return turtle
The dots are stored in a 13✕13 array. Each dot has an attribute, 'type', that determines it status. The edges have a type=None. Occupied dots have a type=True. Unoccupied dots have a type=False.
Your strategy should start with:
def _turtle_strategy(self, turtle):
The turtle argument is a tuple containing the column and row of the current turtle position. That is, turtle[0] is the horizontal position and turtle[1] is the vertical position.
Your strategy should return a tuple containing the column and row of the new turtle position, e.g.,
return [column, row]
There are some resources that you can use in your program, including:
- self._surrounding_dots((column, row))
- returns an array of dots surrounding a given position in the grid
- self._daylight_ahead((column, row))
- returns True if there is a clear path to the edge heading in the current direction
- self._dots
- the array of dots from which you can test the type attribute (self._dots[i].type==None → edge; self._dots[i].type==False → open; self._dots[i].type==True → blocked)
- self._orientation
- you can set the orientation of your turtle by assigning a number from 0-5 (clockwise beginning with 30 degrees from north)
- self._set_label('your message here')
- you can write a message on the toolbar if you want to communicate what your turtle is thinking
- self._grid_to_dot((column, row))
- returns the dot that is at a grid position (column, row)
- self._dot_to_grid(dot)
- returns an array (column, row) representing the grid position of a dot
Where to get Turtle in a Pond
The Turtle in a Pond activity is available for download from the Sugar activity portal: Turtle in a Pond
The source code is available on the Sugar Labs Gitorious server.