Activities/Sliderule

Where to get Sliderule

About Sliderule

"The slide rule also known colloquially as a slipstick, is a mechanical analog computer." This Activity implements a basic slide rule with C, D, A, and L scales and can be used for multiplication, division, roots, addition and subtraction.

The C and D scales are used for multiplication and division.
The A and D scales are used for squares and square roots.
The L scales are used for addition and subtraction.

A nice discussion of the slide rule is found here [1]

The toolbars

From left to right:

project-toolbar button
C scale (multiplication and division)
CI scale (inverse - multiplication and division when the C scale would give underflow/overflow)
A scale (square and square root)
L scale (addition and subtraction)
display of calculation and results
stop button (not shown)

How to use a slide rule

There are three parts to the slide rule: (1) a fixed rule (either the D scale or the L scale); (2) a sliding rule (the A, C, or L scales); and a reticule, which moves independently of the rules.

To move the sliding rules, simply drag them. Also to move the reticule, drag it. (Note: The entire slide rule does not fit on the screen. By dragging on the fixed rule, you can scroll the canvas to reveal different sections.)

Most calculations on a slide rule require three steps:

position the end of the top slide above a number on the bottom slide;
position the reticule over a number on the top slide;
read the result from the bottom slide.

Note: You can read values from the fixed scale from either end of the sliding scale.

The Sliderule Activity displays these three values on tabs attached to the top slider and the reticule. The calculation is also displayed on the activity toolbar.

Note: The scales are all at a fixed scale. It is often necessary to move a decimal place in order to find the number you are looking for on the scale. It is up to the user to keep track and subsequently to estimate the decimal point in the final result.

Note: You typically get 3 significant digits of accuracy when using a slide rule.

Multiplication

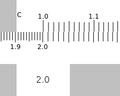
To multiply, you use the log slides, C and D. (Addition in log scale is the same as multiplication in linear space.) First position the end of the C slide over one of the multiplicands on the D slide. Then position the reticule over the other multiplicand on the C slide. Read the result off of the D slide.

Example: 2 × 1.31 = 2.62

Position the end of the C slide over 2 on the D slide
Position the reticule over 1.31 on the C slide and read the results (2.62) from the D slide.

Division

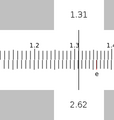
Division is the opposite of multiplication. First position the reticle over the dividend on the D slide. Then without moving the reticule, position the C slide so that the divisor is under the reticule. Read the quotient off of the D slide under the end of the C slide.

Example: 2.62 / 1.31 = 2

Position the reticule over 2.62 on the D slide. Position 1.31 on the C slide under the reticule.
Read the results from the D slide.

Overflow on Multiplication or Division

Sometimes the result of multiplication or division is off the end of the sliderule. For example 4 x 3 or 3/4. Here you can use the CI or inverse scale. To multiply you can divide by the inverse and to divide you can multiply by the inverse.

Square

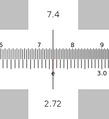
You use the A and D slides to square number. (A is a log-log scale.) Simply position the reticule of number you want to square on the D slide and read the result off of the A slide. (Remember to properly estimate the proper decimal point for your result.)

e² = 7.4

Position the reticule over e on the D slide and read the results off of the A slide.

Square root

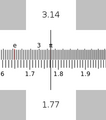
You also use the A and D slides to find the square root of a number. Simply position the reticule of number you want to square on the A slide and read the result off of the D slide. (Remember to properly estimate the proper decimal point for your result.)

√𝜋 = 1.77

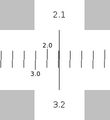
Position the reticule over 𝜋 on the A slide and read the results (1.77) off of the D slide.

Addition

To add you use the linear slides, L and L. First position the end of the top L slide over one of the addends on the lower L slide. Then position the reticule over the other addend on the upper L slide. Read the result off of the lower L slide.

Example: 1.1 + 2.1 = 3.2

Position the end of the upper L slide over 1.1 on the lower L slide.
Position the reticule over 2.1 on the upper L slide and read the result (3.2) from the lower L slide.

Subtraction

To subtract, you also use the linear slides, L and L. Position the reticule over the minuend on the lower L slide. Without moving the reticle, position the upper L slide so that the subtrahend is also under the reticle. Read the difference from the lower L slide.

Example: 3.2 – 2.1 = 1.1

Position the reticule over the minuend (3.2) on the lower L slide and the subtrahend (2.1) on the upper L slide.
Read the difference (1.1) from the lower L slide.

How does it work

Why does multiplication and division work on the C and D scales?

The multiplication of 100 by 1000 can be represented as 10² x 10³ =10⁵, to multiply, just add the indices, in this case, 2+3=5. 2 and 3 are the logarithms of 100 and 1000 respectively.

To multiply, add the logarithms, to divide, subtract. See how the C and D scales are compressed to their right end . Though the scales are marked with numbers, their distance along the scales are proportional to the logarithms of those numbers. When two distances are added, the logarithms of the numbers are added, if logarithms are added, numbers are multiplied.