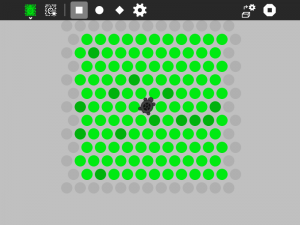
Activities/Turtle in a Pond

Turtle in a Pond Activity

Turtle in a Pond is a strategy game. The goal is to surround the turtle before it runs of the screen.

How to play Turtle in a Pond

Did you know that:

• You can load your own strategy for the turtle

The Toolbars

from left to right

1. the Activity toolbar button (shown in the open position)
2. the New-game button
3. an area for messages
4. the Load-new-strategy button
5. the Reload-the-default-strategy button
6. the Activity stop button

Strategy

In this strategy, the turtle moves down, regardless of whether the dot is open.

def _turtle_strategy(self, turtle):
    turtle[1] +=1
    return turtle

In this strategy, the turtle moves down until it is blocked.

def _turtle_strategy(self, turtle):
    if not self._dots[self._grid_to_dot((turtle[0], turtle[1]+1))].type:
       turtle[1] +=1
    return turtle

In this strategy, the turtle searches for an open dot, looking clockwise.

def _turtle_strategy(self, turtle):
    evenodd = turtle[1] % 2
    for i in range(6):
        column = turtle[0] + CIRCLE[evenodd][i][0]
        row = turtle[1] + CIRCLE[evenodd][i][1]
        if not self._dots[self._grid_to_dot((column, row))].type:
            return [column, row]
    return turtle

In this version, the turtle orientation is set as well.

def _turtle_strategy(self, turtle):
    evenodd = turtle[1] % 2
    for i in range(6):
        column = turtle[0] + CIRCLE[evenodd][i][0]
        row = turtle[1] + CIRCLE[evenodd][i][1]
        if not self._dots[self._grid_to_dot((column, row))].type:
            self._orientation = i
            return [column, row]
    return turtle

In the default strategy, the turtle choose a random direction and goes there if the dot is open.

def _turtle_strategy(self, turtle):
    evenodd = turtle[1] % 2
    n = int(uniform(0, 6))
    for i in range(6):
        column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0]
        row = turtle[1] + CIRCLE[evenodd][(i + n) % 6][1]
        if not self._dots[self._grid_to_dot((column, row))].type:
            self._orientation = (i + n) % 6
            return [column, row]
    return turtle

In this strategy, the turtle will go off the edge if it can.

def _turtle_strategy(self, turtle):
    evenodd = turtle[1] % 2
    for i in range(6):
        column = turtle[0] + CIRCLE[evenodd][i][0]
        row = turtle[1] + CIRCLE[evenodd][i][1]
        if self._dots[self._grid_to_dot((column, row))].type is None:
            self._orientation = i
            return [column, row]

    n = int(uniform(0, 6))
    for i in range(6):
        column = turtle[0] + CIRCLE[evenodd][(i + n) % 6][0]
        row = turtle[1] + CIRCLE[evenodd][(i + n) % 6][1]
        if not self._dots[self._grid_to_dot((column, row))].type:
            self._orientation = (i + n) % 6
            return [column, row]
    return turtle

The dots are stored in a 13x13 array. Each dot has an attribute, 'type', that determines it status. The edges have a type=None. Occupied dots have a type=True. Unoccupied dots have a type=False.

Your strategy should start with:

def _turtle_strategy(self, turtle):

The turtle argument is a tuple containing the column and row of the current turtle position. That is, turtle[0] is the horizontal position and turtle[1] is the vertical position.

Your strategy should return a tuple containing the column and row of the new turtle position, e.g.,

return [column, row]

There are some resources that you can use in your program, including:

self._dots

the array of dots.

self._pressed

the index of the most recent dot pressed by the user

self._orientation

you can set the orientation of your turtle by assigning a number from 0-5 (clockwise beginning with 30 degrees from north)

self._set_label('your message here')

you can write a message on the toolbar if you want to communicate what your turtle is thinking

self._grid_to_dot((column, row))

returns the dot that is at a grid position (column, row)

self._dot_to_grid(dot)

returns an array (column, row) representing the grid position of a dot

CIRCLE

a 2x6x2 array of offsets that can used to find the column and row of the dots surrounding the turtle.

A bit more explanation about the CIRCLE constant:

CIRCLE contains tuples of offsets (a column offset and a row offset) that allow you to find the grid coordinates (column and row) of the 6 dots that surround the turtle. It is complicated by the fact that the rows are staggered (in order to form hexagons) so when the turtle is on an even row (turtle[1] % 2 == 0) we use one set of offsets (CIRCLE[0]) and when it is on an odd row (turtle[1] % 2 == 1) we use a second set of offsets (CIRCLE[1]).

Where to get Turtle in a Pond

The Turtle in a Pond activity is available for download from the Sugar activity portal: Turtle in a Pond

The source code is available on the Sugar Labs Gitorious server.